What on Earth is a matroid – Part 2 – Not-so squiggly lines

This is the second post in a thread introducing matroids. In the last post, we looked at how matroids arise as a natural object in topological graph theory. Now we’re going to attack matroids from the angle of linear algebra. All the while, we’ll push the concepts back into the world of graphs to see what kind of insight this new angle can give us.

Cryptomorphism

That’s a fun word but what does it mean? Essentially it means two systems of axioms are equivalent in the following sense: The objects that satisfy one set of axioms are in one-to-one correspondence with the objects satisfying the other set of axioms, in some kind of ‘natural’ way.

Before we jump back into matroids, one example you might be familiar with is that of topological spaces. Normally, we define a topological space in terms of open sets:

Let $X$ be a set and $\tau$ be a collection of subsets of $X$ that we call ‘open sets’. Then we call $(X,\tau)$ a topoligical space if it satisfies the following axioms:

Both $X$ and $\varnothing$ are open.
The arbitrary union $\bigcup_{i\in I}U_i$ of open sets $\{U_i\}_{i\in I}$ is open.
The intersection $\bigcap_{i\in [n]}U_i$ of finitely many open sets $\{U_i\}_{i\in [n]}$ is open.

But we could equally-well define a topological space as follows: A topological space is a pair $(X,\sigma)$ where $X$ is a set and $\sigma$ is a collection of subsets of $X$ that we call ‘closed sets’ satisfying the following axioms:

Both $X$ and $\varnothing$ are closed.
The arbitrary intersection $\bigcap_{i\in I}U_i$ of closed sets $\{U_i\}_{i\in I}$ is closed.
The union $\bigcap_{i\in [n]}U_i$ of finitely many closed sets $\{U_i\}_{i\in [n]}$ is closed.

These two defintions don’t formally define the same object, but they define equivelent (spiritually the same?) objects in some sense. There is a one-to-one correspondence between spaces defined both ways; we can move easily between them. In particular, a set is closed if and only if its complement is open. This is a cryptomorphism.

Matroids exhibit a multitude of cryptomorphic defintions. In fact, one of the reasons matroids were first studied was as a means of studying equivalence of axiomatic systems.

In the previous post, we saw the following definition for matroids in terms of their ‘circuits’:

A matroid $M=(E,\mathcal{C})$ is a set $E$ called the ground set, along with a set $\mathcal{C}$ of subsets of $E$ called circuits satisfying the following axioms:

(C0) No $O\in\mathcal{C}$ is empty;
(C1) $\mathcal{C}$ is an antichain w.r.t. inclusion. That is, no circuit is a subset of another;
(C2) For distinct $O_1,O_2\in\mathcal{C}$ and $e\in O_1 \cap O_2$ , there is a circuit $O_3\in\mathcal{C}$ s.t. $e\notin O_3$ but $O_3\subseteq O_1\cup O_2$ .

The last condition is called circuit elimination. Subsets of $E$ which contain circuits are called dependent and those which do not contain circuits are called independent.

But we could have just as well stated the definition in terms of ‘bases’. This next definition will help us understand why matroids are a kind of generalisation of linear algebra.

Bases

A matroid $M=(E,\mathcal{B})$ is a set $E$ called the ground set, along with a set $\mathcal{B}$ of subsets of $E$ called bases satisfying the following axioms:

(B1) There is at least one base. That is, $\mathcal{B}\neq \varnothing$ ;
(B2) For distinct $B_1,B_2\in\mathcal{B}$ and $e\in B_2\setminus B_1$ , there is an element $f\in B_1\setminus B_2$ s.t. $B_2-e+f$ is a base.

The last condition is called basis exchange and is inspired by the properties of bases from linear algebra. We can get between the cryptomorphic defintions in the following way:

Given a matroid axiomatised in terms of circuits (minimally dependent sets), we obtain bases as the maximally independent (circuit-free) sets. Given a matroid axiomatised in terms of bases, we obtain circuits as the minimally dependent sets.

Like in a vector space, we can prove that all bases in a (finite) matroid have the same size.

Recall that, from a matroid $M$ , we obtain the dual matroid $M^*$ by taking its bases to be the complements of all of the bases of $M$ .

It sounds like “matrix”

As you might expect, the independent and dependent collections of vectors in a vector space satisfy the axioms of a matroid. In fact, we can be a little bit broader with this. If we take a matrix $A$ , with entries in some field $\mathbb{F}$ , then we can consider the columns as ground set elements, with the independence/dependence relations of the column space (treating the columns as vectors). Note that this is a little more general than the vector space defintion, since we might have columns that have the same entries but, by virtue of being differet columns, give multiple ‘parallel’ ground set elements.

Now we have a way to express elements of non-graphic matroids. Remember that a graphic matroid is a matroid on the edge set of a graph, whose circuits are the cycles of the graph. In particular, recall the forbidden minors from Tutte’s characterisation of graphic matroids:

$M^*(K_5)\quad M^*(K_{3,3})\quad U^2_4\quad F_7\quad F_7^*$

None of these matroids are graphic, but the matroid $F_7$ can be expressed as a matrix over $\mathbb{F}_2=\{0,1\}$ as follows:

$\begin{bmatrix} 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 & 1 \end{bmatrix}$

Graphic matroids are representable as matrices over any field. Given a graph $G=(V,E)$ , assign an arbitrary orientation to all of the edges (decide for each edge a ‘source’ and ‘target’ vertex). Now define a matrix as follows: Each row corresponds to a vertex $u\in V$ . Add a column for each edge $e\in E$ , with entries all $0$ except for a $1$ at the target of $e$ and a $-1$ at the source of $e$ . Remember that in the field $\mathbb{F}=\mathbb{F}_2=\{0,1\}$ , we get $-1=1$ . The matroid that this matrix defines is (isomorphic to) the cycle matroid $M(G)$ of the graph.

How about $U^2_4$ , the ‘uniform matroid of rank 2 on 4 elements’? We’ve been keeping awefully quiet about the representations of this one. In general, the uniform matroid $U^r_n$ is the matroid on the ground set $\{1,\ldots,n\}$ with bases exactly the subsets of size $r$ .

It turns out that $U^2_4$ is has no matrix that represents it with entries in $\mathbb{F}_2$ (or any field of characteristic 2). We can, however represent $U^2_4$ over $\mathbb{F}_3=\{-1,0,+1\}$ .

This is a strange phenomenon and it brings us to our next section.

Representability

We say that a matroid $M$ is representable over a field $\mathbb{F}$ if it is generated as the ‘column matroid’ of some matrix with entries in $\mathbb{F}$ .

It turns out that the matroids representable over $\mathbb{F}_2$ , the so-called binary matroids, are exactly those which do not contain $U^2_4$ as a minor.

Similarly, the ternary matroids, those representable over $\mathbb{F}_3$ , are characterised by the following set of four forbidden minors:

$U^2_5\quad U^3_5=(U^2_5)^*\quad F_7\quad F_7^*$

The matroids representable over every field are called regular matroids and it turns out that regular matroids are exactly those which are both binary and ternary. Therefore, the regular matroids are characterised by the forbidden minors:

$U^2_4\quad F_7\quad F_7^*$

These kind of representability results are tied together into Rota’s Conjecture below. It is sometimes seen as the matroid-theoretic counterpart to graph theory’s Robertson-Seymour Theorem.

Rota’s Conjecture – For any finite field $\mathbb{F}$ , the set of forbidden minors that characterise the matroids representable over $\mathbb{F}$ is finite.

In 2013, Geoff Whittle announced that he, along with Jim Geelen and Bert Gerards, had solved Rota’s conjecture. The result has yet to be published.

While I’d like to dive further into the representability of matroids, I’ll leave this here and maybe come back to it in a future post.

Rank

What other ideas from linear algebra can we import into matroid theory? Well, since for a finite matroid, all of its bases have the same size, we automatically get a notion of ‘dimension’. We call this size value the rank of a matroid $M$ and denote it by $r(M)$ .

We can extend this notion of rank to a function on all subsets of the ground set. Indeed, for a matroid $M$ on a ground set $E$ , the rank of a subset $F\subseteq E$ is the size of the largest independent set contained within $F$ and is denoted $r(F)$ .

For matroids that come from vector spaces, the rank of a subset is the dimension of the subspace generated by that set.

We even get a cryptomorphic definition of matroids via the rank function:

A matroid $M=(E,r:\mathcal{P}(E)\rightarrow\mathbb{Z}_{\geq0})$ is a set $E$ called the ground set, along with a function $r:\mathcal{P}(E)\rightarrow\mathbb{Z}_{\geq0}$ that assigns to subsets of $E$ an integer rank, satisfying the following axioms:

(R1) For all subsets $F\subseteq E$ , we have $r(F)\leq |F|$ ;
(R2) Rank is submodular. That is, for any subsets $A,B\subseteq E$ , we have $r(A\cup B)\leq r(A)+r(B)-r(A\cap B)$ ;
(R3) Rank is monotonic. That is, for any subset $F\subseteq E$ and any $e\in E$ , we have $r(F)\leq r(F\cup\{e\})\leq r(F)+1$ .

The rank of a matroid $M=(E,r)$ is then $r(E)$ . The bases of $M$ are the subsets of maximum rank.

Rank allows us to define another familiar structure! We get the analogues of linear subspaces, hyperplanes. In matroid-land, these are called flats and are the subsets of the ground set $E$ that are maximal with their current rank. That is, we can’t add any more elements without increasing their rank. These flats form an ordered set (a lattice in fact!), which leads to another way to cryptomorphically define a matroid. Sadly, we don’t have time to go into that now.

Let’s bring it back to graphs

What role does rank play in the cycle matroids of graphs? It seems like a strange property to try and query graphs about, but it turns out to make some graph definitions more elegant.

Recall that the bases of a cycle matroid of a connected graph $G=(V,E)$ correspond to the edge sets of the spanning trees (the maximally acyclic subgraphs in $G$ ). In this way, we get $M(G)$ has rank $|V|-1$ .

From this, the flats of a graph $G$ are the ‘induced subgraphs’ of $G$ . That is, the subgraphs defined on a specific set of vertices with as many edges from the parent graph included as possible.

This is cool but not particularly enlightening. What is more interesting, is when we look at graph connectivity in terms of matroids…

Let $G=(V,E)$ be a graph. For some number k, we say that a collection of k vertices $S\subseteq V$ is a k-separator of $G$ , if removing the vertices $S$ leaves $G$ disconnected. A graph is called k-connected if it has no k-separator.

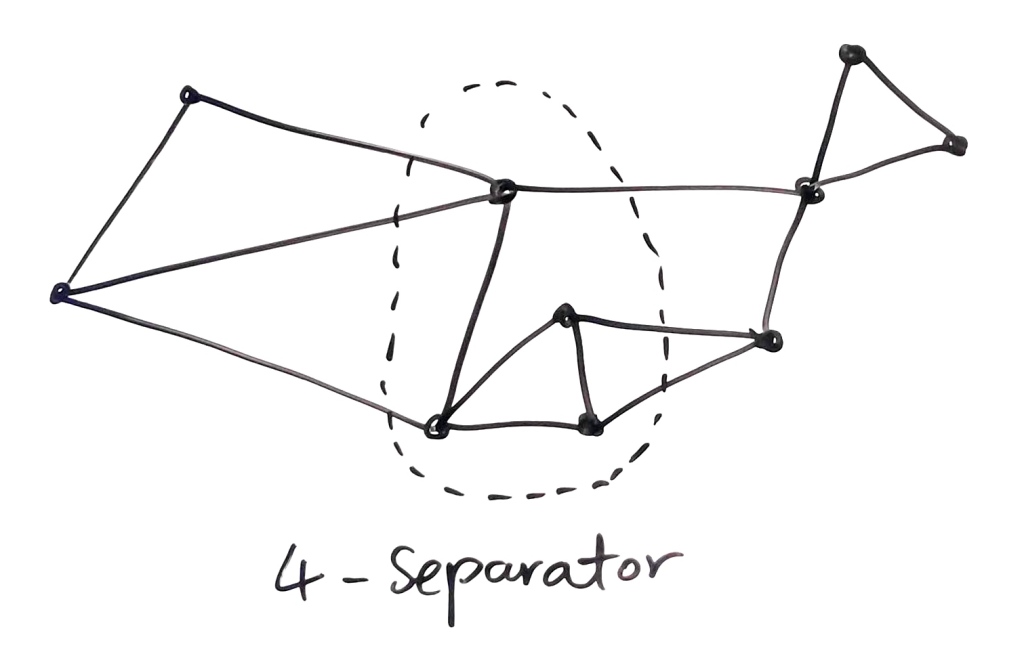
In the spirit of matroids, let’s try and rewrite this in terms of edges. How about:

Let $G=(V,E)$ be a graph. A nontrivial bipartition of the edge set $E=A\cup B$ is called a separation of $G$ . We say that it is a k-separation if the total vertices incident with $A$ and the total vertices incident with $B$ have k vertices in common. A graph is k-connected if it has no k-separation.

Now, these definitions aren’t one-to-one (a separation gives a unique (minimal) separator but not always vice versa) but they’re close enough for our purposes. Indeed, the definitions of k-connected coincide (at least when there are sufficient vertices involved).

We can lift the separation defintion straight to matroids using rank. Indeed, for a set of edges in a cycle matroid, rank counts one less than the number of vertices incident with those edges.

Let $M$ be a matroid on a ground set $E$ . A separation of $M$ is a bipartition of the ground set $E=A\cup B$ . We say that it is a k-separation if $r(A)+r(B)+1=r(M)+k$ . We say that a matroid is k-connected if it has no k-separation.

As you would expect, k-separations of cycle matroids correspond to k-separations of the graphs that generated them (except when the original graph is not connected). As such, lots of graph-connectivity results generalise to matroids. We can even define tree-decompositions (and thus treewidth) of matroids using this machinery!

That’s the end of this post for now, but I hope to explore this all again in detail soon.

Will's place for things