Generalising obstructions – Part 1 – Nestedness

This is the first blog post in a collaborative project between me and Ben Bumpus, whose blog can be found here. We’re looking to use category theory to generalise machinery from the theory of obstructions to tree decomposition. I plan to make a separate post introducing category theory (with a graph theory twist of course) sometime soon. If that doesn’t exist yet, I can recommend S. Awodey’s book (available for free online). For this post, you’ll need a basic understanding of categories, natural transformations, products and pullbacks.

Ben and his co-authors have already made significant inrows into the subject of generalising tree decompositions. At some point there’ll be an accessible introduction on Ben’s blog but, for now you can check out their first paper here.

Intro

Graph theory can be messy; there can be a lot of data and sometimes there’s no symmetry to work with. Luckily, there are lots of tools that can help us make sense of complicated graphs. Tree decomposition, for example, splits up a graph $G$ into lots of subgraphs that are glued back together to form $G$ in a “tree-like way”. Amongst other things, tree decompositions are closely tied to separators and separations of graphs, which we explore in the next section.

Separations and corners

In a graph $G$ , a separation is a cover of the vertex set $A\cup B=V(G)$ such that each edge of the graph lies completely in one of the sets $A$ or $B$ . We call a separation ‘trivial’ if one of its sides is contained in the other. We’ve got to be carfeul with this definition; sometimes separations are defined on the edge set (as in a previous post). For our purposes however, it will be more convenient to define separations on vertex sets. We say that a separation $A\cup B$ is of order $k$ if $|A\cap B|=k$ and in this case we call it a $k$ -separation.

Separations allow us to chop up our graph into simpler pieces; they’re everywhere in structural graph theory, but is it useful to consider all separations of a graph? Perhaps in a few cases, but in general we want to be more specific, so that we have information about how the separations interact. Consider a long cycle for instance; even if we just consider separations of order two, there is one of these for every pair of vertices. It’s worth taking some time to think about why this doesn’t lead to a nice decomposition; would it even make sense to split our graph up along all of these? If not, how do we make a canonical choice of separations out of all the possibilities?

To this end, we make the following definition: We say that a separation $A\cup B$ is nested with a separation $C\cup D$ if we have $A\subseteq C$ and $B\supseteq D$ or the same arrangement after swapping the order of either separation. If separations aren’t nested, then we call them crossed.

Crossed separations aren’t as nice as nested ones, but this is ok; a pair of crossed separations gives rise to four new ‘corner’ separations which may be nicer than the originals. Let $G$ be a graph and consider a pair of crossed separations $A\cup B$ and $C\cup D$ . The four corner separations are

$(A\cup C,B\cap D)$ , $(A\cup D,B\cap C)$ , $(A\cap D,B\cup C)$ and $(A\cap C,B\cup D)$ .

If the separations a set of separations $S$ are pairwise nested with eachother, we call $S$ totally nested.

Structured decompositions

You can find a full introduction to structured decompositions here. For now though, we can understand them as follows: Given a category $\mathcal{C}$ , a ( $\mathcal{C}$ -valued) structured decomposition $d$ is a diagram in $\mathcal{C}$ whose shape is governed by a some graph $G$ . That is, for each vertex $u$ of $G$ we have an object $du\in\mathcal{C}$ and for every edge $e$ in $G$ , that spans vertices $u$ and $v$ , we have an object $de\in\mathcal{C}$ along with monic (injective) arrows $du\leftarrow de\rightarrow dv$ (a ‘monic span’).

Morphisms between structured decompositions are natural transformations between the diagrams. In this way, we get a category $\mathcal{D}\mathcal{C}$ of $\mathcal{C}$ -valued structured decompositions.

Observe that structured decompositions with tree shape, valued in the category of reflexive graphs and homomorphisms, are exactly tree decompositions of graphs!
In fact, if we take the colimit of a graph-valued structured decomposition, it glues everything together into one object, which turns out to be the underlying graph!

We can easily represent separations in this language too: A separation of a graph $G$ is a structured decomposition $d$ of shape $P_1$ (two vertices with an edge spanning them), whose colimit is (isomorphic to) $G$ .

Now, before we get to the punchline, we need one more defintion.

The right universe

What if we want to investigate exactly the structured decompositions that have got something to do with a particular colimit $G$ ? We’ll need a category of such things if we want to do category theory on them. This brings us to the definition below. We’ll put this definition in more context in a future post.

Given a category $\mathcal{C}$ and an object $c\in\mathcal{C}$ , we define the category $\text{fract}(c)$ as follows: The objects of $\text{fract}(c)$ are colimit cocones $x\rightarrow c$ from some diagram $x$ to its colimit $c$ . We call these the fracturings of our object $c$ . Morphisms between $a:x\rightarrow c$ and $b:y\rightarrow c$ are given by natural transformations $f:x\rightarrow y$ such that $b\circ f=a$ .

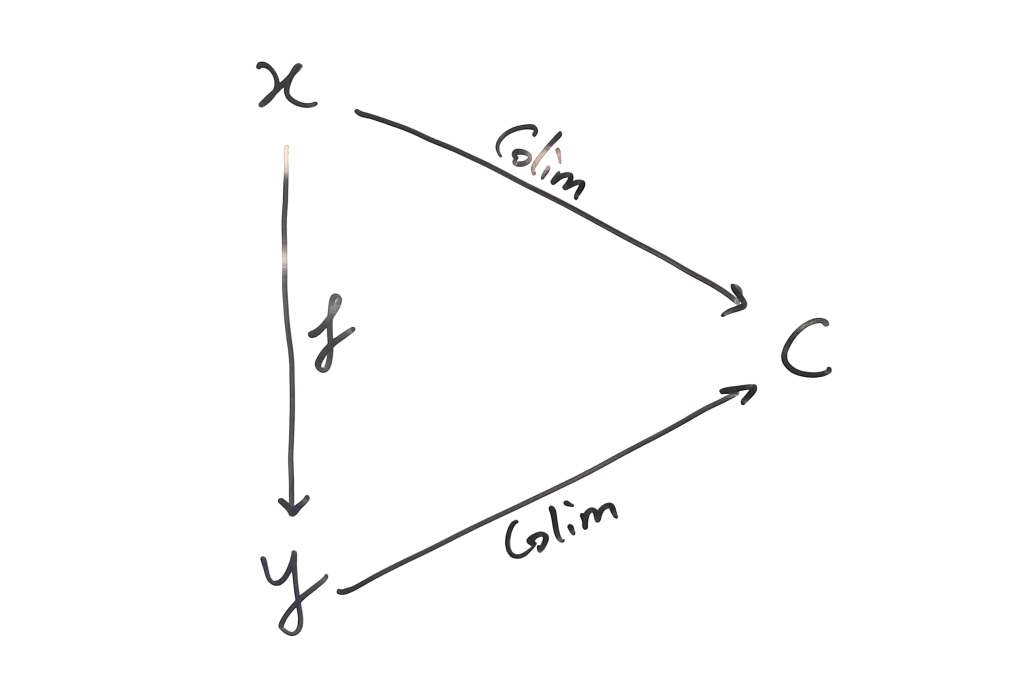
Structured decompositions live in this category, but so do diagrams of other shapes. Sometimes we’ll restrict ourselves further so that we are only dealing with diagrams of particular shapes.

Back to nestedness!

Right away, we can make a fun observation: Given a graph $g$ in the category $\underline{\text{Gr}}$ of reflexive graphs and graph homomorphisms, let’s work in the category $\text{fract}(g)$ . Given separations (in our new context), $s_1$ and $s_2$ , there is a span $s_1\leftarrow p\rightarrow s_2$ where $p$ is a decomposition of shape $P_2$ . Since this is concise, lets turn it into a definition for structured decompositions in general.

Definition: In the category $\text{fract}(g)$ , we say two structured decompositions $s_1$ and $s_2$ of shape $P_1$ are nested if there is a structured decomposition $p$ of shape $P_2$ that spans $s_1$ and $s_2$ .

Why don’t we try messing around with limits in this category to see what happens? For now, we’ll see what happens to structured decompositions of shape $P_1$ .
Observe that products in $\text{fract}(g)$ are just pullbacks in the original category with respect to the base object $c$ and the morphisms into it.

Let $d_1,d_2$ be two objects in $\text{fract}(g)$ , that have shape $P_1$ :

$d_1x\leftarrow d_1e\rightarrow d_1y$ and $d_1x\leftarrow d_1e\rightarrow d_1y$

Let’s try and calculate the product of these. We’ll need the following category theory fact:

Fact: Limits of diagrams have the shape of the limit of their underlying graphs (in the category of reflexive graphs and homomorphisms).

Using this, all we need to do is know how to take the pullback of a graph, right? Not quite! It’s actually much simpler. Since the diagram $g^\ast$ containing just the graph $G$ has one vertex, namely $G$ , it is the shape of the terminal graph, and so the pullback is simply a product.

This product will have nine objects, four corresponding to the combinations of the different images of $x$ and $y$ , which we will denote by $dxx,dxy,dyx$ and $dyy$ , and five corresponding to the other object combinations. We’ll get the following diagram and we’ll use the fact that it commutes to determine what the objects actually are:

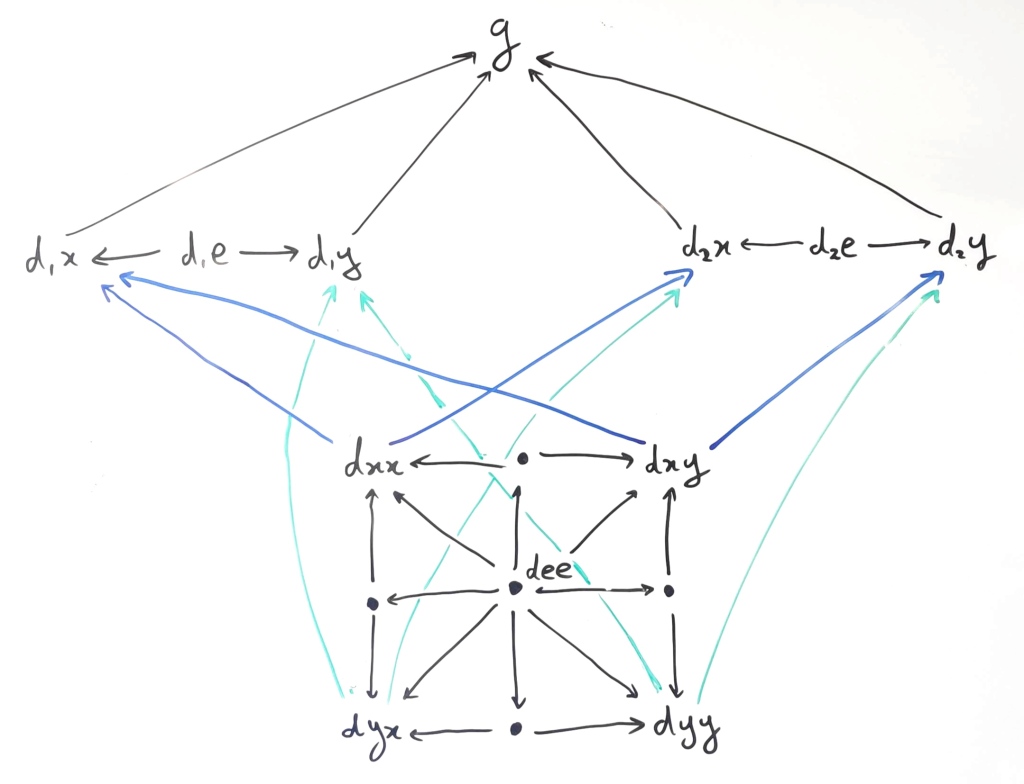
For each $w,z\in{x,y}$ we’ll get that $dwz$ is the pullback of $d_1w$ and $d_2z$ with respect to their inclusion into $G$ . Thus $dwz$ will be the intersection of these graphs. The other objects will represent intersections between the objects of $d$ that the maps that leave them span.

If you pause for a moment to look at the diagram above, you might begin to see something familiar. It seems like we’ve run into corners! Indeed, the objects $dxx, dxy, dyx, dyy$ are exactly the corners of the crossing separations (if they cross).

What happens if they don’t cross? Well, if the separations we started out with were nested, we’d get one of the corners is empty.

This is exactly what we’d expect. Why? Because if separations are nested, then there is a span with top of shape $P_2$ . By the universal property of the product, this needs to factor through the product. The only way that it can do this is if one of the corners is empty.

This is neat, and maybe it lends itself to further generalisation. Stay tuned while we iron out the details…

2 responses to “Generalising obstructions – Part 1 – Nestedness”

Generalising obstructions – Part 2 – Fracturings – Will's place for things

June 13, 2023 at 4:09 pm

[…] a collaborative project between me and Ben Bumpus, whose blog can be found here. The first post is here. We devoted a week to messing around with the categorical machinery and now have a little […]

LikeLike

Tree Decompositions via Lattices – Merlin’s Notebook

June 13, 2023 at 4:21 pm

[…] separations and fracturings of objects of a category; you can read about these things on his blog here and […]

LikeLike