Generalising obstructions – Part 2 – Fracturings

This is the second blog post in a collaborative project between me and Ben Bumpus, whose blog can be found here. The first post is here. We devoted a week to messing around with the categorical machinery and now have a little collection of lemmas and a clearer direction. Lots of stuff didn’t work like we thought it might and there are a couple of things that seem like nice results but might not fit into the larger project anymore. This post is devoted to recording some of those things. It will be a little disjointed but I hope you’re able to get something out of these ideas. Ben has written a parallel post about one of our findings here. Watch out for more intallments (both here and on Ben’s blog) – we’ll be documenting our new ideas sometime soon.

In the previous post, we saw how we can express nestedness of separations in the language of category theory. In the following section, we generalise this.

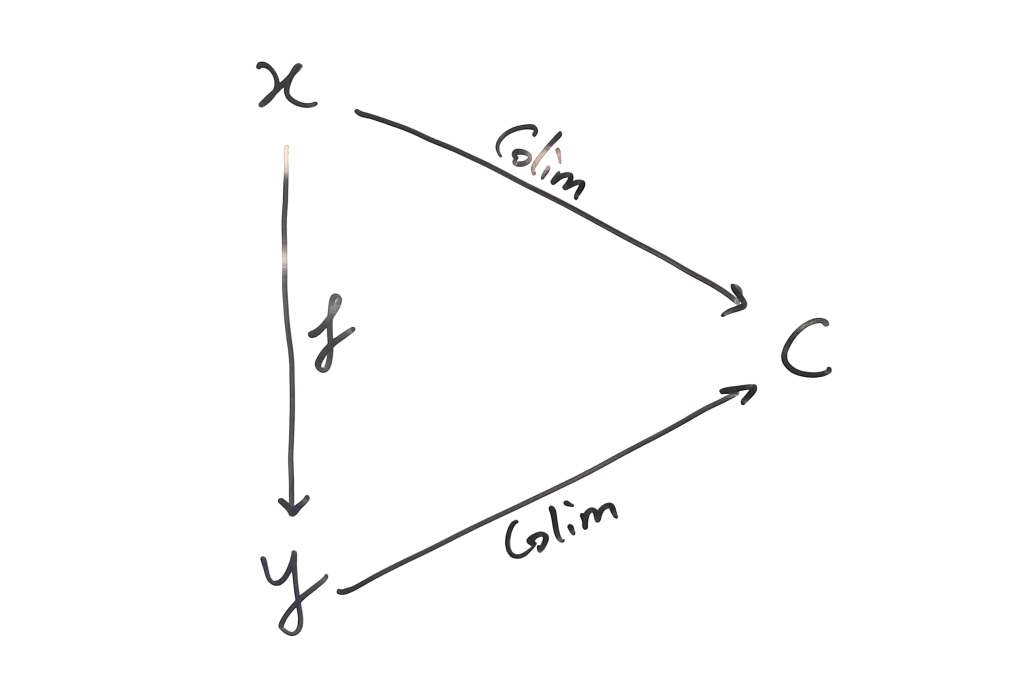
First though, let’s recap the setting. We can think of a separation of a graph as a really simple tree decomposition, one with two bags and one adhesion. We can think of a tree decomposition of a graph $G$ as a diagram in the category of graphs; we have objects corresponding to bags, objects corresponding to adhesions and monic spans from these adhesions to their bags:

The diagram’s colimit (when we glue it all together) must be $G$ .

We write $\text{fract}(c)$ (fracturings of $c$ ) for the category of diagrams whose colimits are some object $c$ . Morphisms in this category are natural transformations that commute with the colimit cocones:

Interlacing

Recall that, in the category $\text{fract}(c)$ of fracturings of an object $c$ , two separations $S_1$ and $S_2$ are nested if there is a span $S_1\leftarrow P\rightarrow S_2$ where $P$ has shape $P_2$ . The intuition of this can be thought of as follows:

The span tells us that the $P_1$ -shape decompositions are actually just coarser versions of a $P_2$ -shape decomposition and they are somehow ‘lined-up’.

This definition seem to be a bit restrictive though. Shouldn’t we be able to say that $P$ can have any path shape? This doesn’t quite work. Indeed, given crossed separations $S_1$ and $S_2$ , it might be that a path of length three ( $P_3$ ) factors through $S_1\times S_2$ as follows:

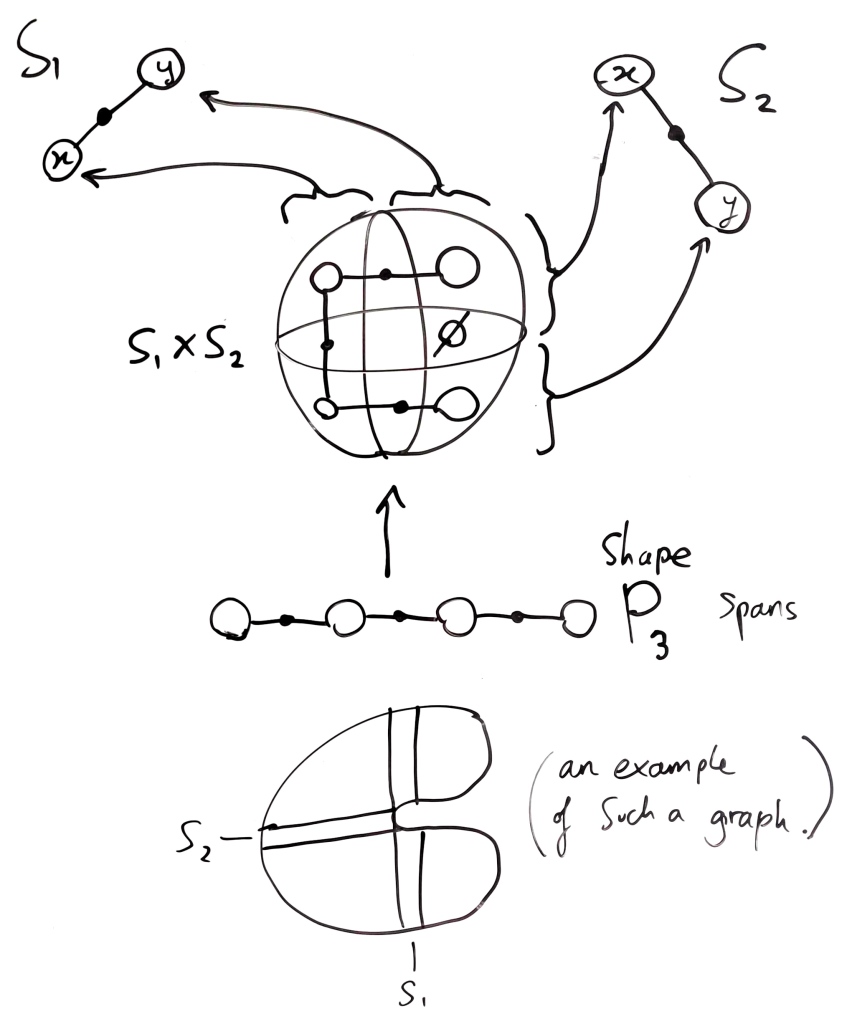
Since it factors through the product, it spans $S_1$ and $S_2$ .

So what’s going wrong in this example? Well, the map from $P$ into $S_2$ somehow ‘folds in on itself’. In fact, this is precisely the problem. Let’s make the following definition.

Definition We say that a map $a\rightarrow b$ between fracturings is a contraction map if the map on the shapes of the decompositions is a contraction map. That is, if it just consists of contracting edges and identifying the end bags.

Now we can make the following generalisation:

Definition We say that two separations $S_1$ and $S_2$ are nested if there is a span of contraction maps $S_1\leftarrow P\rightarrow S_2$ where $P$ has path shape.

But why stop there? Why settle for boring-shaped decompositions?

Definition We say that a class $\mathcal{F}$ of graphs is closed under subdivision. If for any $G\in\mathcal{F}$ and $H$ a subdivision of $G$ , we have $H\in\mathcal{F}$ .

Definition Let $\mathcal{F}$ be a graph class closed under subdivision. We say that two fracturings $F_1$ and $F_2$ with shapes in $\mathcal{F}$ are $\mathcal{F}$ –interlaced if there is a span of contraction maps $F_1\leftarrow F\rightarrow F_2$ where $F\in\mathcal{F}$ .

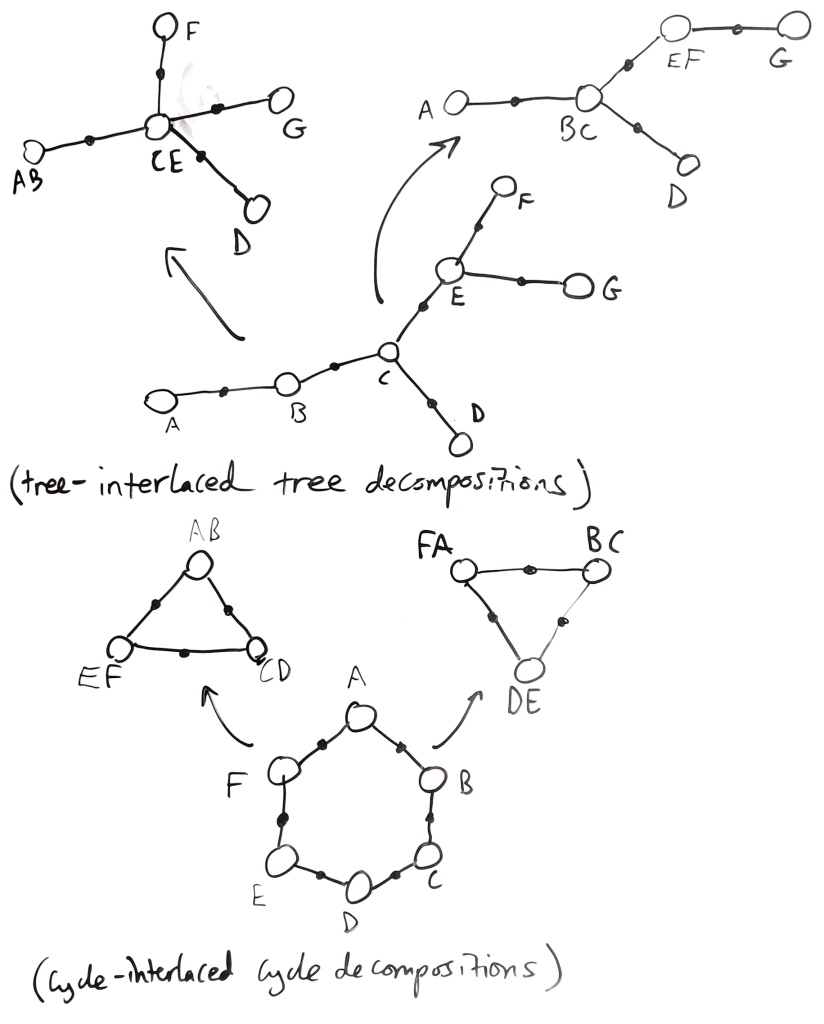
In particular, nestedness of separators is interlacedness of fracturings with respect to the class of paths.

This machinery possibly has some nice applications to the mechanics of refining decompositions of a particular class of shapes. But we’re going to leave it here for now.

We found out more stuff about corners

Given a pair $S_1$ and $S_2$ of crossed (non-nested) separations, we can obtain four new separations, the “corner separations” from the intersections and unions of pairs of sides of the separations.

These corners are used in the theory of separations to refine systems of separations and have all sorts of nice properties.

Oberve that we can get corner separations via the following means:

Observation Let $Z$ be a separation such that $S_1\times S_2\rightarrow Z$ . Then either $Z=S_1,S_2$ or $Z$ is a corner separation.

That is, there are six unique ways to contract the product to a fracturing of shape $P_1$ .

One of the nice properties of corners is that any separation $S$ , that is nested with both of $S_1$ and $S_2$ , is nested with all four corner separations. This follows immediately from our above obersvation.

Let’s play around with limits some more. Suppose we are given crossing separations $S_1,S_2$ and a separation $S$ nested with both. Let $P$ and $Q$ be nestedness-witnessing paths of length two for the pairs $S_1,S$ and $S,S_2$ respectively. Let’s take the pullback over $P\rightarrow S\leftarrow Q$ .

Observe that $P\times_S Q$ factors uniquely into the product $S_1\times S_2$ since it maps into both $S_1$ and $S_2$ . To figure out the shape of $P\times_S Q$ , we split into two cases based on exactly how these witnessing spans are:

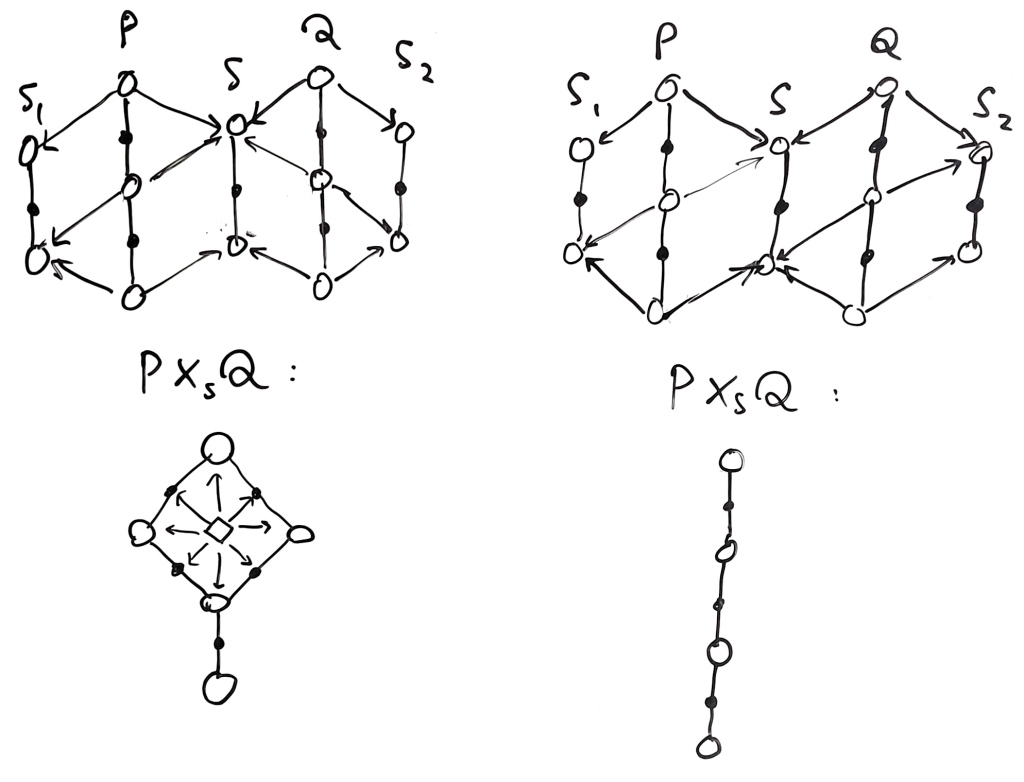
We can ommit the second case; indeed, this is telling us that $S_1$ and $S_2$ were nested in the first place. The first case is the interesting one. We obtain this “tadpole”-shaped diagram that contains both the information about the product and the separation $S$ . In fact, the shape of the diagram gives us a canonical choice for which corner is “closest” to the separation $S$ . This normally requires a lot of poset machinery. That’s pretty neat!

That’s all for now. Keep an eye open for more installments soon!

One response to “Generalising obstructions – Part 2 – Fracturings”

Tree Decompositions via Lattices – Merlin's Notebook

June 20, 2023 at 2:00 pm

[…] I had an absolute blast. Will and I proved a bunch of new results and this post is about one of them: I’ll tell you how to deifne tree decompositions in terms of lattices of subgraphs. I think that it’s a cute result in of itself, but also that it will have profound consequences in the future. If you’re interested, Will has written a pair of posts about separations and fracturings of objects of a category; you can read about these things on his blog here and here. […]

LikeLike

Will's place for things